Рейтинг: 4.4/5.0 (1520 проголосовавших)Категория: Инструкции
При развертывании поверхности на плоскости каждой точке поверхности соответствует единственная точка на развертке: линия поверхности переходит в линию развертки; длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями, остаются неизмеренными. Таким образом, процесс построения развертки сводится к отыскиванию натуральной (истинной) величины каждого элемента поверхности и изображению их на плоскости.
Каждая боковая грань на развертке строится как треугольник по трем сторонам. CS — самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.
Для нанесения на развертку точек D, Е и F . соответствующих вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники АBС и DEF . дающие истинную величину основания и сечения пирамиды.
На рис. 149 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Sum. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.
Рис. 149 Поверхность двенадцатиугольной пирамиды
Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 149. От оси симметрии S - 0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две стороны равны истинным величинам образующих, а третья — хорде, стягивающей дугу окружности основания между соседними точками деления. Построенные на развертке точки О, 1, 2. соединяются. Построение развертки значительно упрощается, если поверхность представлена прямой пирамидой правильной формы или прямым круговым конусом. На рис. 150 приведена развертка четырехгранной прямой пирамиды. Построение ее упрощается тем, что образующая пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее спроецировались в натуральную величину.
Рис. 150 Развертка четырехгранной прямой пирамиды
Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить сторону AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А. соответственно получим точку В и т. д. Основание же в натуральную величину можно построить на базе одной из его сторон (на рис. 150 — на базе стороны АВ ). Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М2 ) проведем горизонтальную линию до пересечения с ребрами A2 S2 и B2 S2 . Получим точки 11 и 22. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 1, 2.
На рис. 151 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S. радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку.
Рис. 151 Пример построения развертки прямого кругового конуса
Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки M2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку M2 . Расстояние от основания конуса до точки M2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.
Здесь мы начинаем публикацию материалов по предмету начертательная геометрия. Статьи находятся в стадии разработки, в настоящее время заполняется раздел по черчению. В будущем на той странице появятся уроки и пошаговые инструкции по решению задач. Надеемся, что с помощью них позиционные задачи и метрические задачи для вас перестанут быть нерешаемыми. Кроме того, мы постараемся в доступном виде объяснить азы начертательной геометрии, научимся строить проекцию точки, проекцию прямой, проекции плоскости. Наиболее сложной начертательная геометрия выглядит в первые дни, особенно если преподаватели относятся к своей работе без должного энтузиазма. На этих страницах мы постараемся раскрыть те нюансы, которые ускользнули у вас во время занятий по инженерной графике
Уроки по начертательной геометрии. Инженерная графика и начертательная геометрия 1 курс.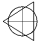
Определение линии пересечения треугольной призмы и полусферы.
Дата добавления: 2010-05-18
В этом уроке мы рассмотрим задачу, в которой требуется найти линии пересечения призмы и полусферы, определим их видимость.
Дата добавления: 2010-09-30
Одна из главных тем позиционных задач курса начертательная геометрия - определение точки пересечения прямой общего положения с плоскостью общего положения.
Дата добавления: 2010-10-12
В этом уроке мы разберем алгоритм, позволяющий построить линию пересечения двух плоскостей, заданных треугольниками. Эта задача практически гарантированно встретится вам в ходе изучения начертательной геометрии.
Прежде чем приступить к построению проекций геометрических тел, ознакомимся со способами нахождения проекций точек, расположенных на поверхностях многогранников и тел вращения.
Нахождение проекций отдельных точек, расположенных на поверхности тел, рассмотрим на трёх простейших геометрических формах: пирамиде, конусе и шаре. Нахождение горизонтальных проекций точек при заданных вертикальных их проекциях рассмотрим одновременно для пирамиды и конуса.
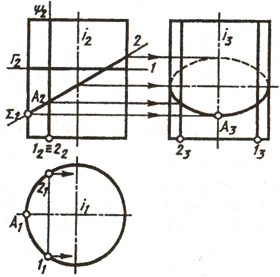
Пусть пирамида и конус (фиг. 119, а, б) даны двумя своими проекциями, а точки А и В, лежащие на поверхностях этих тел, заданы своими вертикальными проекциями а' и b'. Требуется найти горизонтальные и профильные проекции этих точек.
Такие задачи можно решать следующим способом: на поверхности тел через заданную точку и вершину фигуры проводится прямая линия и затем строятся проекции этой прямой. Искомая горизонтальная проекция точки будет лежать на горизонтальной проекции прямой. На фиг. 119, а и 119, б через точку b' проведена вертикальная проекция s'k' вспомогательной прямой линии SK. Как видно, вертикальной проекции s'k' соответствует горизонтальная проекция sk, что позволяет построить горизонтальную проекцию точки В. После этого легко построить профильную проекцию точки b''.
Чтобы построить горизонтальную проекцию точки А для пирамиды, нет необходимости строить вспомогательную прямую, так как точка А по заданию лежит на ребре S2. При наличии профильной проекции пирамиды легко построить профильную проекцию а" точки А на профильной проекции ребра S2 и по ней построить горизонтальную проекцию а. Если профильной проекции на чертеже нет, надо использовать следующее основное положение начертательной геометрии: если точка а'
делит отрезок s'2' в отношении s'a'/a'2'=m/n, то и на горизонтальнои проекции будет sa/a2=m/n. Вычислив по вертикальной проекции отношение ™, можно легко найти горизонтальную проекцию точки А на S2.
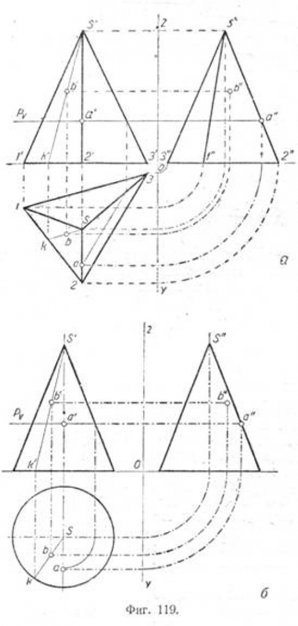
Эта задача может быть решена способом секущих плоскостей, являющимся общим для любой пространственной формы. Если провести через вертикальную проекцию точки А секущую горизонтальную плоскость P, то она пересечёт пирамиду по треугольнику, подобному треугольнику основания (фиг. 119, а), a конус или шар (фиг. 119, б и 120) — по кругу. В этом случае треугольник и круг сечения проектируются на горизонтальную плоскость в натуральную величину. Горизонтальные проекции точки A расположены одновременно на перпендикулярах к оси ОХ, опущенных из соответственных вертикальных проекций точки A.
При выполнении упражнений по проекционному черчению приходится довольно часто решать задачи на построение линий пересечения друг с другом двух поверхностей. Для выполнения этих построений необходимо уметь находить точки входа и выхода прямых, пересекающих заданные поверхности. Рассмотрим это построение на примерах.
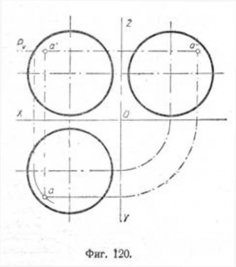
Пусть даны проекции пирамиды, конуса, шара и прямые EF и MN, пересекающие эти тела. Прямая EF перпендикулярна к плоскости V, а прямая MN—к плоскости W (фиг. 121, а, б, в). Требуется построить точки входа и выхода прямых, пересекающихся с заданными поверхностями.
Проводим через прямые EF и MN горизонтальные секущие плоскости: через прямую EF—плоскость P, а через прямую MN—плоскость Q. Эти плоскости образуют на горизонтальной плоскости проекций пирамиды и конуса в сечении фигуры, подобные их основанию, а для шара— круг. Точки пересечения прямых с контурами сечения и будут искомымй точками входа и выхода: для прямой EF—точки А и С, а для прямой MN—точки К и L.
Если прямая пересекает поверхность шара, пирамиды или конуса перпендикулярно к плоскостй Н, то в этом случае проводят через заданную прямую фронтальную плоскость. С целью упрощения построений для пирамиды и конуса полъзуются горизонтально-проектирующей плоскостью, которая должна непременно проходить через вершину фигуры.
Построив затем на вертикальной плоскости проекций, соответственно секущей плоскости, контуры сечения, находят точки входа и выхода.
Примеры решения задач на построение проекций фигур
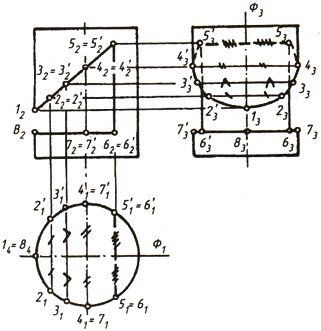
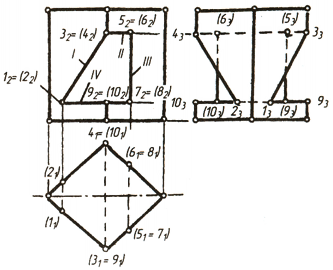
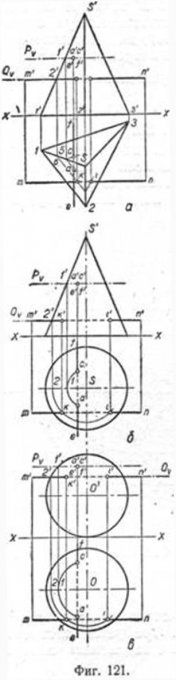
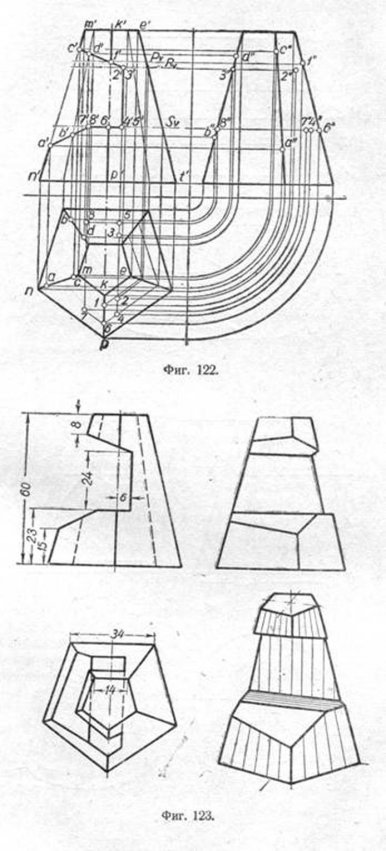
Пример 1. На фиг. 122 даны три проекции пятиугольной усечённой пирамиды с открытым вырезом, образованным несколькими секущими плоскостями. Сечением этих плоскостей образовано на поверхности пирамиды ряд характерных точек: С, D, 1, 2, 3, 4, 5, 6, 7, 8, В и А, которые на вертикальной плоскости проекций отмечены соответственно: c', d', 1', 2', 3', 4', 5', 6', 7', 8', b' и a'. Требуется построить горизонтальные и профильные проекции этих точек.
Проекции точек А, В, С и D могут быть легко определены, так как они расположены на рёбрах пирамиды. Определим, для примера, горизонтальную проекцию точки С, лежащую на ребре MN. Для этого проведём из точки с' проектирующую линию до пересечения с горизонтальной проекцией ребра MN и определим таким образом горизонтальную проекцию с точки С. Имея вертикальную и горизонтальную проекции этой точки, можно построить и профильную проекцию с". По аналогии с этим, строим проекции точек А, В и D. Проекции остальных точек 7, 2, 3, 4, 5, 6, 7 и 8 строим способом секущих плоскостей.
Чтобы построить горизонтальную проекцию, например точки 7, проводим через неё секущую плоскость P, которая пересечёт пирамиду по пятиугольнику, подобному её основанию. Чтобы не затемнять чертежа построением пятиугольника, ограничимся одной из его сторон, проектирующейся на грань KETP. Пересечение контура сечения с горизонтальной проекцией ребра KP даст горизонтальную проекцию точки 1. Горизонтальные проекции точек 2, 3 определяются по аналогии, т. е. проведением через 2' и 3' плоскости R. Подобным образом производится построение остальных точек. Имея горизонтальные и вертикальные проекции всех точек, нетрудно построить их профильные проекции. Законченное построение пирамиды приведено на фиг. 123. К изображениям в ортогональных проекциях добавлена аксонометрическая проекция этой пирамиды.
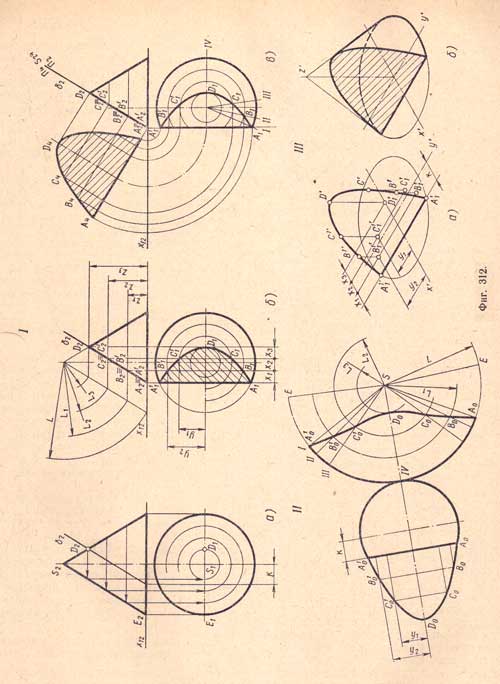
Пример 2. Построение в усечённом конусе вырезов,образованных четырьмя плоскостями, пересекающими поверхность конуса по основным кривым: окружности, эллипсу, параболе и гиперболе, приведено на фиг. 124. Горизонтальные проекции точек А и 1, лежащих на вертикальной проекции линии контура конуса, легко определить без дополнительных построений. Проекции остальных точек найдены проведением горизонтальных секущих плоскостей, обозначенных следами Pv,Rv и т. д.
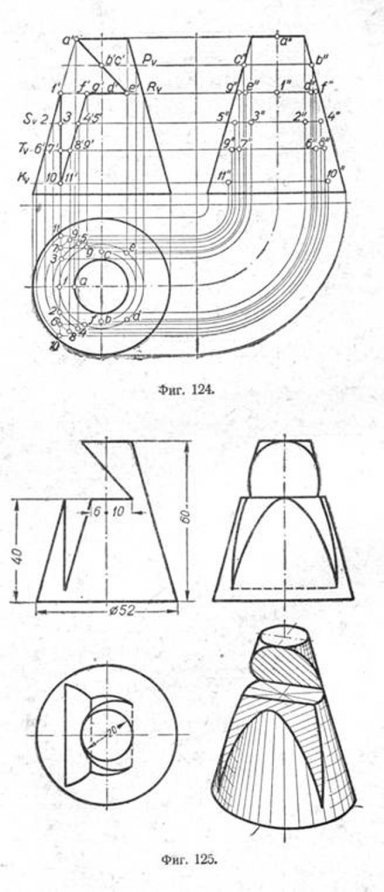
Определив горизонтальные проекции точек, нетрудно построить их профильные проекции. Последовательное соединение проекций точек кривых сечения показано на фиг. 125. Там же даны размеры конуса. Рядом с ортогональными проекциями показан тот же конус в диметрической проекции.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Стоимость и возможные формы обучения (очно или дистанционно) смотрите разделе Цены.
Подробнее о репетиторстве.
Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.
Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:
Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник .
УпражнениеДана пирамида, основание которой параллельно ?1. Основание представляет собой некоторый треугольник.
S – вершина пирамиды (Рисунок 6.1).
Рисунок 6.1 – Пересечение поверхности пирамиды прямой
Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.
Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость ?).
Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.
Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.
Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).
Рисунок 6.2 – Построение развёртки пирамиды
В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.
6.2. Призма. Развертка призмыПризма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях .
УпражнениеДана призма, основания которой параллельны плоскости проекций ?1 .
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).
Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы
Рассмотрим наклонную призму. Пусть основание призмы параллельно ?1. а ребра параллельны ?2 .
Построим нормальное сечение, то есть сечение плоскостью ?, перпендикулярной ребрам призмы (Рисунок 6.4).
Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.
Рисунок 6.4 – Построение развёртки призмы
В результате пересечения многогранников получим ломаную линию.
Возможны два случая пересечения многогранников (Рисунок 6.5):
Рисунок 6.5 – Варианты пересечения многогранников
Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.
Звенья ломаной – линии пересечения граней .
Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.
Построенные точки соединить.
УпражнениеПостроить линии пересечения призмы с пирамидой (Рисунок 6.6).
Рисунок 6.6. Построение линии пересечения призмы с пирамидой
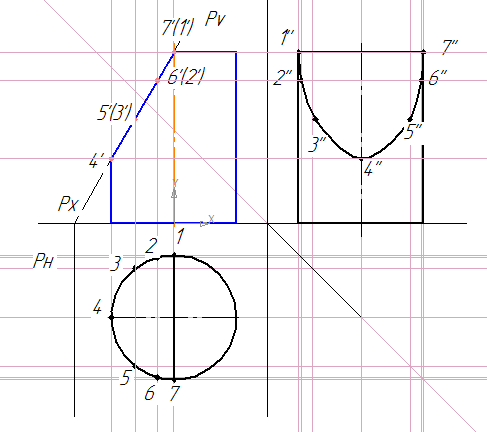
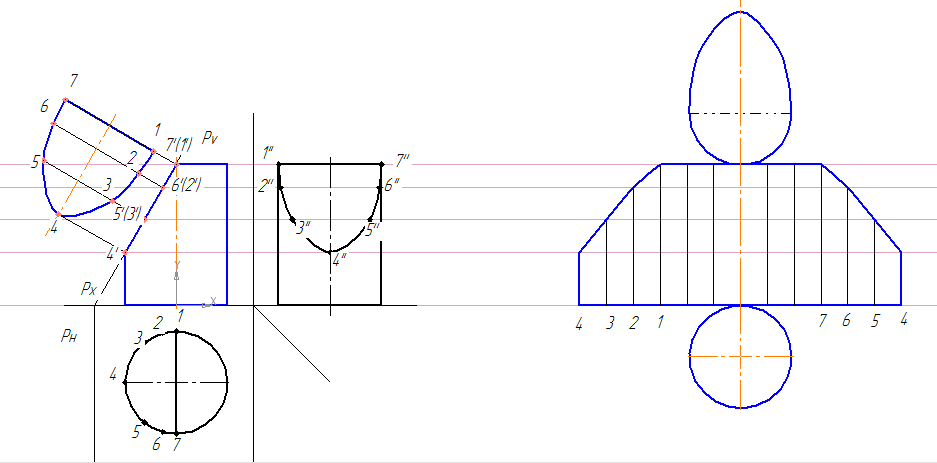
Построить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Это сечение пересекается:
— с ребром D в двух точках 1 и 4;
— с ребром Е в двух точках 2 и 5.
Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.
Построение развертки рассмотрено ранее.
6.4. Задачи для самостоятельной работы1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Стоимость и возможные формы обучения (очно или дистанционно) смотрите разделе Цены.
Подробнее о репетиторстве.
При построении развертки пирамиды применяется метод треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.
Рисунок 137. Определение истинной величины основания и ребер пирамиды
Алгоритм построения можно сформулировать следующим образом (рис. 137):
определяют натуральную величину основания пирамиды (например, методом замены плоскостей проекций);
определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S );
с троят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рис.138).
Рисунок 138. Построение развертки пирамиды
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки.
Примером первой точки на рисунках служит точка К0 и К О SАD . а иллюстрацией второго случая являются точки М0 и М0 *. Для определения точки К0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ ( метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S0М0 и, наконец, точки К0 .
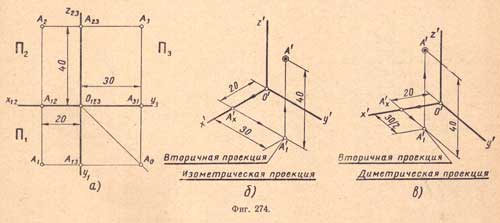
Рассмотрим систему трех взаимно перпендикулярных плоскостей проекций (рис. 5): П1 горизонтальная плоскость проекций, П2 фронтальная плоскость проекций и П3 профильная плоскость проекций.
Рис. 5. Плоскости проекций:
Точка пересечения трех плоскостей O123 – начало координат. Линия пересечения горизонтальной и фронтальной плоскостей называется осью проекций x12 = П1 ? П2. линия пересечения горизонтальной и профильной плоскостей называется осью проекций y13 = П1 ? П3. линия пересечения фронтальной и профильной плоскостей называется осью проекций z23 = П2 ? П3 .
Поскольку плоскости проекций бесконечны, три плоскости разделят все пространство на восемь частей – октантов. Порядок отсчета октантов (см. рис. 5): слева от плоскости П3 (против часовой стрелки) с первого по четвертый, справа – с пятого по восьмой .
Направление осей x,y,z в первом октанте считается положительным. Знаки осей, продолженных за начало координат, считают отрицательными.
Для получения проекций точки А на три плоскости (рис. 6) П1. П2 и П3 через точку А проводятся проецирующие лучи [AA1 ) – до пересечения с плоскостью П1. [AA2 ) – до пересечения с плоскостью П2 и [AA3 ) – до пересечения с плоскостью П3. Точка A1 – горизонтальная проекция точки. A2 – фронтальная проекция точки. A3 – профильная проекция точки. Точки A12 A13 A23 – вспомогательные, лежащие соответственно на осях x,y,z .
Рис. 6. Проецирование точки на три плоскости проекций
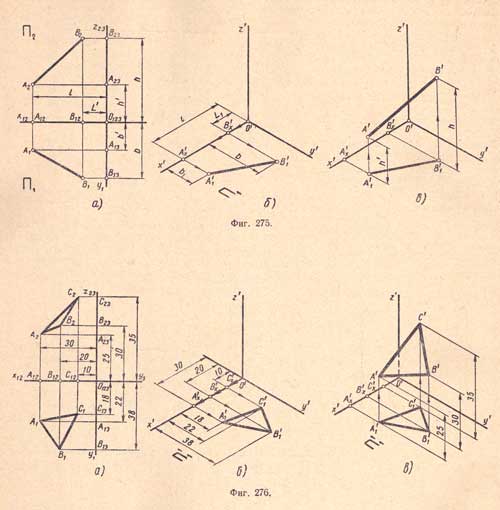
Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси x по часовой стрелке, а плоскость П3 – вокруг оси z до совмещения с П2. Плоскость П2. точки A2 и A12 остаются неподвижными (рис. 7), точки A1 и A13 и ось y1 поворачиваются вместе с П1. После поворота, точки A1. A2 и A12 образуют вертикальную линию связи. Точки A3 и A23. поворачиваясь вместе с П3 и осью y3. образуют, после поворота, горизонтальную линию связи A2 A3. Точки A1 и A3 соединяются ломаной линией связи A1 A0 A3. Вершина ломаной линии связи или точка преломления A0 лежит на биссектрисе угла y1 O123 y3. Множество вершин ломаных линий связи определяют условную линию, называемую постоянной прямой комплексного чертежа k123 .
Рис. 7. Трехкартинный комплексный чертеж точки:
Чертеж трех совмещенных плоскостей проекций называется трехкартинным комплексным чертежом. Метод образования комплексного чертежа называют методом Монжа, в честь французского ученого Гаспара Монжа, жившего в XIX веке, первым предложившего использовать совмещенные чертежи.
Для решения задач в начертательной геометрии часто используются чертежи на двух совмещенных плоскостях проекций, которые называются двухкартинными комплексными чертежами (рис. 8).
Рис. 8. Двухкартинный комплексный чертеж точек, занимающих различное положение относительно плоскостей проекций
